最近はいろんな情報が溢れかえっていて
どの情報を参考にすればいいのか
的確に選び出すのは難しいものです。
エントロピーって?
エントロピーという単語を
聞いたことがありますか?
私も昔に勉強したのですが
結局のところ、
よくわからないままでした。
「エントロピー」でGoogle検索をすると
検索画面のトップに以下のように
表示されます。
エントロピー
Google検索画面より
原子的排列および運動状態の混沌(こんとん)性・不規則性の程度を表す量。
机の上のエントロピー
堀淳一氏の著書
「物理の風景 数理物理学者の見た世界」によりますと、
机の上に物が雑多に積み上がってくると
物理学者は
「机の上のエントロピーが大きくなった」
と表現するそうです。

机の上のエントロピーが大きいって
つまり、どういうこと?
雑多で乱雑に散らかっている状態は
エントロピーが大きいという事ですね。
逆に、物が整然とキレイに
並んでいる状態は
エントロピーが小さいという事になりますね。
エントロピーは自然に増加する
例えば、
容器を隔壁で2つに分け
片方に気体を入れ、
片方を真空にしたとします。
この状態から隔壁を取り除くと、
あとは人間が手を加えずとも
気体は容器全体に行き渡ります。
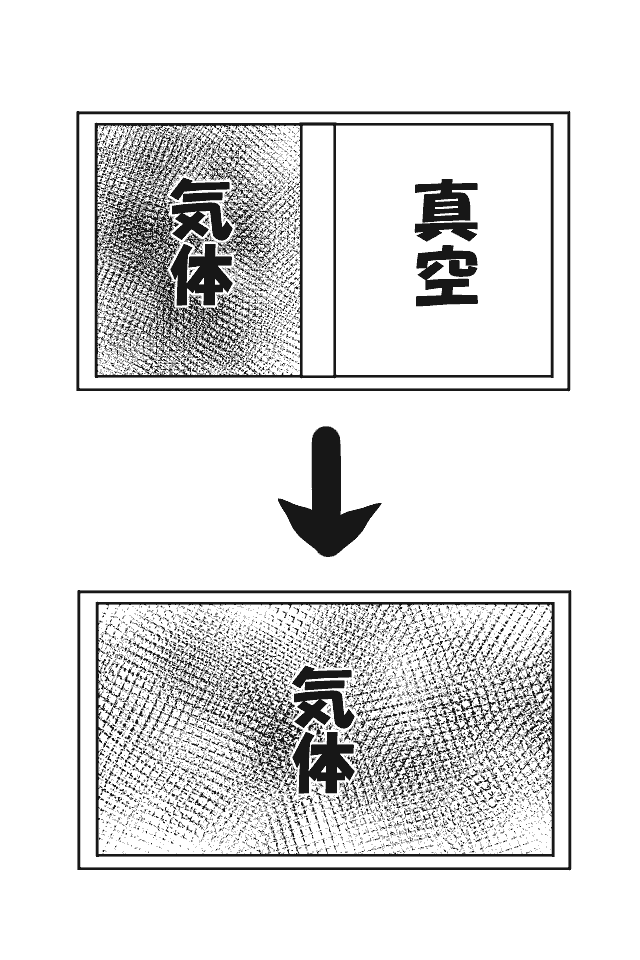
隔壁を取り除く前と比較すれば
気体の分子が飛び回れる範囲が
広がっており、
エントロピーが大きくなっています。
しかし、容器全体に行き渡った気体は
何も手を加えなければ
自然と容器の片方に戻る事はありません。
自然に生じる変化は
常にエントロピーが増大する方向に
向かって起こるのです。
情報の拡散も同じ!?
近年はネットの発達により
情報はあっという間に拡散されてしまいます。
そして一旦広がってしまった情報は
元に戻る事はありません。
これは、先程の気体の例と
よく似ているように思います。
日々、新しい情報が生まれては
どんどん広がっていく。
今では夥しい情報が乱雑に
溢れかえっています。
これも情報のエントロピーが大きくなった
という事でしょうかね。
情報量とエントロピー
情報量について
事象Eが起こる確率をP(E)とすると、
情報量I(E)は
$$I(E)=-\log P(E)$$
引用元
https://ja.wikipedia.org/wiki/情報量
尚、対数の底は2を選ぶ事が多いので
以下、底は2で計算します。
例えば、以下のようなくじ引きに
1回だけ挑戦するとします。
99パーセントの確率で当たり、
1パーセントの確率でハズレが出る
ここでハズレを引き当てた時の情報量は
$$-\log_2 0.99 \simeq 0.0145$$
当たりを引き当てた時の情報量は
$$-\log_2 0.01 \simeq 6.64$$
「当たりを引いた」という情報の方が
情報量が圧倒的に大きくなっています。
このくじ引きの場合は
ほとんどハズレとなっているため、
ハズレを引いたとしても
「なんだ、ただのハズレか・・・」
と思うだけで特に重要さを感じられませんが、
当たりを引いた場合は、
起こりにくい方の事象が発生した事になるため、
その情報はハズレに比べれば
重要さを感じられます。
つまりは起こりにくい事象が起きたら
情報量が大きいというわけです。
エントロピー
情報量のエントロピーH(P)は、
各事象Aに対して
$$H(P)=-\sum_{A} P(A)\log P(A) $$
簡単に言ってしまえば
得られる情報量の期待値となりますね。
先程のくじの場合は
各事象Aは「当たり」か「ハズレ」の
2通りしかないので、
$$ -(0.99\log_{2} 0.99) – (0.01\log_{2} 0.01) \simeq 0.08$$
エントロピーは大体0.08になります。
では、今度はくじの確率を
当たり:50%
ハズレ:50%
に変えてみましょう。
すると情報のエントロピーは
$$ -(0.5\log_{2} 0.5) – (0.5\log_{2} 0.5) = 1$$
となり、エントロピーが大きくなりました。
各事象が均等な確率で起こる状態では
エントロピーが大きくなります。
各事象が均等な確率で起こるという事は
それは秩序がなく乱雑、
どんな情報が出てくるか最も予想が難しい
状態という事です。
情報が溢れかえった社会
書籍、テレビ、ネットなど
今の社会は情報が
乱雑に溢れかえっています。
しかし、
そんな状況だからこそ
そこから情報を探し出す事には
やり甲斐があるとも言えるのかもしれません。
Googleのような検索エンジンの重要性
ネット上の膨大な情報の中から
必要な情報を自力で
探し出すのは骨の折れる事です。
しかしGoogleの検索窓に
調べたい事を打ち込めば
あっという間に必要な情報を
絞り込んでくれます。
ネットで価値の高い情報を得るために
検索エンジンの重要性は
非常に高いと言えますね。
ツイッターの雑多アカウント
私のツイッターアカウントでは
主に株式投資、イラスト、ゲーム制作、
ラブライブ、ダンメモ、ガルパ、
その他気になった情報など
色々と気になった事を
雑多につぶやいています。
所謂「雑多垢」です。
私が勝手にそう思っているだけで
もしかしたら他者から見たら
違うように見えているかも
しれませんが・・・
そうすると、
私のツイッターアカウントは
発信する情報が乱雑で
エントロピーが大きいという
事になるのでしょうね。
エントロピーが大きい事が
良いか悪いかはさておき
情報発信する際には
意識してみるのは面白いかもしれません。
まとめ
情報のエントロピーがどうのこうの
書きましたが、要は
雑多に溢れかえっている情報の中から
必要な情報を探し出す事に対する
価値は高まっているのではないでしょうか。
って話です。
拙いとはいえブログを
書いている身としては
価値ある情報を提供できるように
なりたいと思っていますが、
現実は中々シビアなものですねぇ(汗
そして、
雑多な情報の中から
必要な情報をあっという間に
絞り込んでくれる
Google検索に感謝です(^^
いつも助かってます。