20歳で半分終わってる！？人生の残り時間は案外少ないかも

こんにちは。slashです。
今回は人生の残り時間についてのお話です。

20歳で人生は半分終わっている！？

平均寿命

厚生労働省の調査によりますと
日本人の平均寿命は

だそうです。

引用元URL
https://www.mhlw.go.jp/toukei/saikin/hw/life/life17/index.html

『20歳で人生は半分終わっている』とはどういう事か？

見出しに20歳で人生は半分終わっている、
と書きました。

普通に考えると確かにその通りです。

ここでは計算の簡単化するため
男女共に80歳まで生きるとします。

単純に計算すれば
人生の折り返し地点は

$$80\div2=40$$

40歳となりますが・・・
これを体感時間で考えると話が変わってきます。

ジャネーの法則

ジャネーの法則によりますと、
人の体感時間の長さは年齢に逆比例する
とされています。

年齢が2倍になれば
体感時間の長さは1/2になる。
↓
時間が2倍早く過ぎているように感じる

つまり、年齢を重ねると
時間が早く過ぎているように
感じるようになるというわけです。

出典：ウィキペディア
https://ja.wikipedia.org/wiki/ジャネーの法則

体感時間ベースでの人生の折り返し地点は？

先ほどのジャネーの法則を踏まえて
体感時間ベースで人生の折り返し地点を考えてみます。

年齢と体感時間の長さ

年齢：x
体感時間の長さ：y

とすると、
人の体感時間の長さは年齢に逆比例するので

$$y=\frac{1}{x}$$

反比例の数式になりますね。
（比例定数は1としておきます。）

縦軸を体感時間の長さy
横軸を年齢xとして
グラフにすると大体こんな感じです。

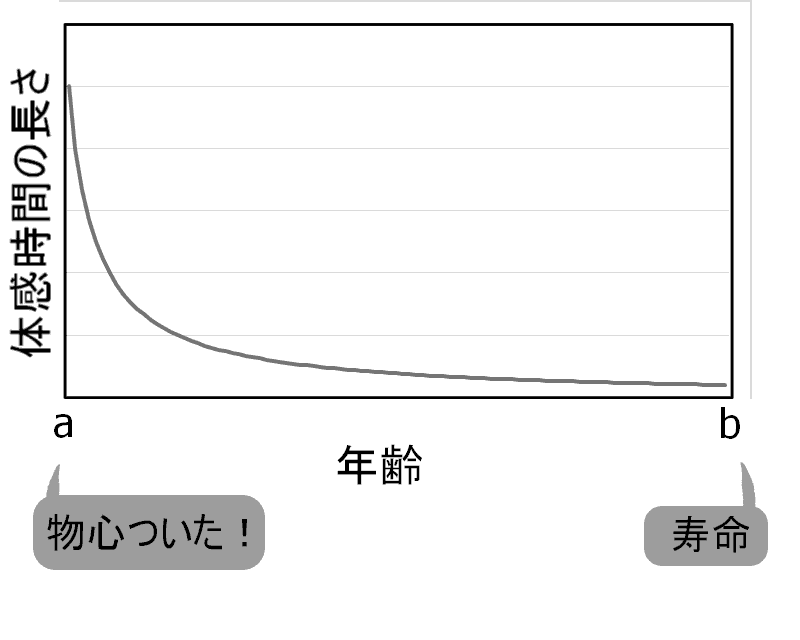
累積の体感時間

物心ついた時の年齢：a
寿命：b
現在の年齢：c

とすると、
物心ついた時の年齢aから現在の年齢cまでの
累積の体感時間は、
下にある図2の斜線部分の面積となります。

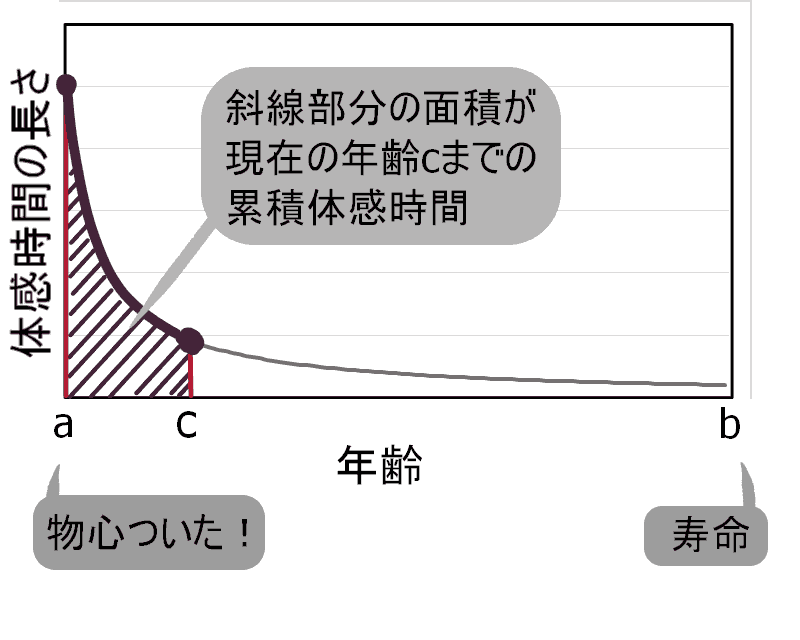
ということは、
先ほどの反比例の数式を
aからcまで積分すれば求められます。

$$\int_a^c \frac{1}{x}dx 　…(A)$$

この数式を(A)とします。

また、
物心ついてから寿命を迎えるまでの
累積の体感時間は

$$\int_a^b \frac{1}{x}dx 　…(B)$$

この数式を(B)とします。

体感時間ベースの折り返し地点

体感時間ベースの折り返し地点を求めるには
先ほどの(A)の結果が
(B)のちょうど1/2になるように
現在の年齢cを求めればいいのです。

人生の折り返し地点を計算する

反比例の数式を積分すると

$$\int \frac{1}{x}dx = \log |x| + 積分定数$$

このようになります。
現在の年齢cまでの累積体感時間(A)は

$$\log c -\log a$$

寿命bを迎えるまでの累積体感時間(B)は

$$\log b -\log a$$

となります。
対数計算の公式で

こういうのがありますので、
この公式を使うと
現在の年齢cまでの累積体感時間(A) と
寿命bを迎えるまでの累積体感時間(B)はそれぞれ

$$(A)=\log(\frac{c}{a})$$

$$(B)=\log(\frac{b}{a})$$

となるので、
体感時間ベースでの人生の折り返し地点は
先ほども書いたように
(A)の結果が
(B)のちょうど1/2になるように
現在の年齢cを求めればいいので

$$(A)=\frac{1}{2}\times(B)$$

$$\log(\frac{c}{a})=\frac{1}{2}\times\log(\frac{b}{a}) $$

ここでまた対数計算の公式ですが

この公式を適用して

$$\log(\frac{c}{a})=\log(\frac{b}{a})^\frac{1}{2}$$

logを外して

$$(\frac{c}{a})=(\frac{b}{a})^\frac{1}{2}$$

あとは順次変形していくと

$$c=a\times(\frac{1}{a})^\frac{1}{2}\times b^\frac{1}{2}$$

$$c=a\times(a)^{-\frac{1}{2}}\times b^\frac{1}{2}$$

$$c=a^{\frac{1}{2}}\times b^\frac{1}{2}$$

$$c=\sqrt{a}\times\sqrt{b}$$

$$c=\sqrt{ab}$$

かなりコンパクトな数式になりました。
これが体感時間ベースでの人生の折り返し地点です。

久しぶりに積分やら対数やらの計算をしたので
なんか間違ってたらゴメンナサイ

実際に数値を当てはめてみる

ここに数値を当てはめてみましょう。

物心つくときの年齢：a=4歳
寿命：b=80歳

このように仮定すると、

$$c=\sqrt{4\times80}=\sqrt{320}=17.89$$

四捨五入してキリの良い数値にすると18歳

なんと！体感時間では
18歳という若さで人生の折り返し地点に
到達してしまいます！

寿命：b=100歳

としてもう一度計算しなおしてみると

$$c=\sqrt{4\times100}=\sqrt{400}=20$$

100まで生きる仮定でも
20歳という若さで折り返しです！

いやはや、驚きの結果ですね。
20歳になる頃には
体感では人生は半分終わってるわけですね。

もちろんこの結果は
ジャネーの法則が正しい事が前提になりますし
また、物心ついた時の年齢や
寿命なども大雑把に仮定して
かなり雑に計算したものとなります。

とりあえず、
体感時間ベースで考えると
人生の折り返し地点はかなり早い段階で迎える
という事がなんとなくわかって頂ければ良いかと思います。

最も重要な事：この結果を受けてどうするか？

体感時間ではかなり早い段階で
人生は半分終わっている
という結果を見て

・・・で終わっていてはあまり意味がありません。
この結果を受けて、
それを活かそうとしなければ
ムダな知識が1個増えただけで終わってしまいます。

この結果に不安や危機感を覚えるなら
何らかの行動を起こした方がいいと思います。

例えば

「老後なんてあっという間に来るからそこに向けて資金を蓄えよう」

「人生は思った以上に短いんだからチャレンジできる事は早めにチャレンジしておこう」

「時間を無駄にしないように有意義に過ごす方法を考えよう」

今回の結果を受けて
このように思って行動を始められたなら
それは意味があったと言えるでしょう。

まぁ、こんな事を偉そうに書いてる
私自身も時間を有意義に過ごせているか
微妙なところなので（笑）
これからの人生の時間を
有意義に過ごせるようにしていきたいと思います。

おわり