資産運用で味方につければ頼もしい！指数関数

こんにちは、slashです。
新年明けましておめでとうございます。
2020年最初の記事です。

さて、挨拶はこの辺にしておき
今回は資産運用で是非とも味方につけたい
指数関数のお話です。

指数関数とは？

指数関数は以下のような式で表されます。

$$ y=a^x $$

xが変数でaは定数です。
a>1であればxが増加するにつれて
yも増加していきます。

ドンドン加速する指数関数的な伸び

先程の指数関数をxについて微分すると

$$ \frac{dy}{dx}=(\ln{a})a^x $$

a>1であれば
その導関数もxが増加するにつれて
増加していきます。
つまり、xが増えれば
yが増加するペースが
ドンドン上がっていくコトになります。

指数関数のグラフを描くとこんな感じです。

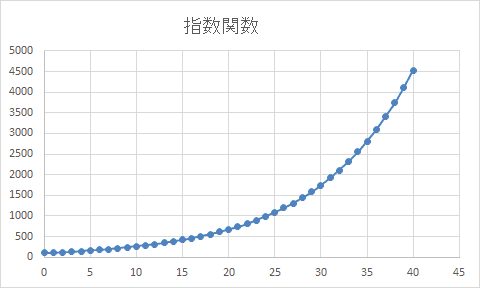
xの値が小さいところでは増加が遅いですが、
xが増加していくと
yの増加が加速しているのがわかります。

指数関数を味方につける資産運用

この性質は資産形成をする上でも
知っておきたいものです。

ところで、複利効果というものを
聞いた事がありますでしょうか？

資産運用で得た利益を
再投資することで
利益が利益を生み出し、
資産の増加が加速していく！
というアレです（汗

例えば、100万円を年5％の利益で
運用すると仮定します。
1年運用すると100万円の5％（＝5万円）の利益を加算して、
資金は105万円となります。

この5万円の利益も再投資し、
さらにもう1年運用したら
105万円の5％（＝5.25万円）の
利益を加算して、資金は110.25万円となります。

こうして、3年目、4年目・・・と
長く運用していくと
資産の増加スピードが上がっていき、
大きな資産が形成できるわけです。

30年も運用すれば
資金は約432万円にもなります。
元の4倍以上ですね。

バフェットの資産推移は指数関数的

特にこの複利効果を
最大限に活かしたのが
投資の神様と呼ばれる
ウォーレン・バフェットですね。

そこでバフェット氏の資産推移を見てみましょう。

バフェット氏の年齢を横軸、
資産総額（ドル）を縦軸で
グラフを描いてみるとこんな感じです。

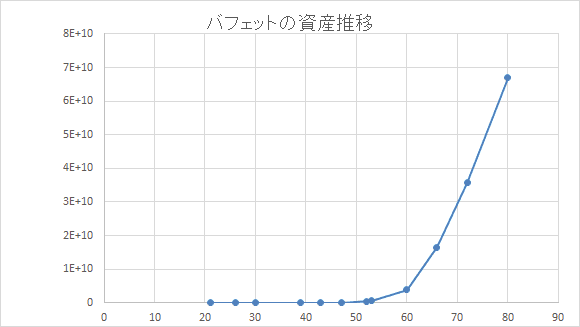
50歳を過ぎたあたりから
急激に伸びるような形になっています。
80代では資産は約670億ドルという
途方も無い大きさにまで
膨れ上がっています。

50代以降の伸び方が凄い一方で
40代あたりまでは
このグラフではほとんど
動きが無いように見えます。

そこで
40代以前の資産の推移を
よくみるためにグラフの縦軸を
対数軸に変えてみましょう。

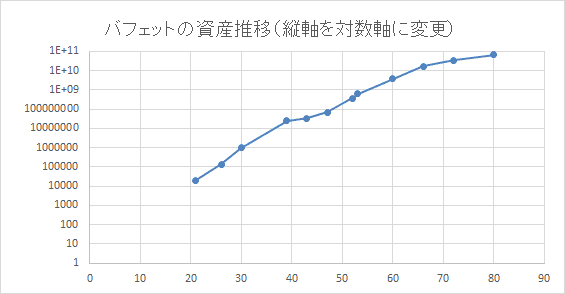
対数軸だと20代の約20000ドルから
右肩上がりに増加しているのが
よくわかりますね。

まさしく指数関数的な資産の増え方です。

一般人の資産形成はどうすればいい？

私を含め、
世の中のほとんどの人は
バフェットほどの
資産を築き上げる事はできないでしょう。

しかし、大半の人は
何百億ドル（日本円にすれば1兆円超え！）
ほどの資産は必要ないはずです。

しかし、数千万円くらいの
資産は築きたいものです。
これを書いている私も
数千万円程度資産を持ちたいと
思っておりますが
思うだけでは実現しないので、
行動を起こす必要があります。

投資で増やすのであれば
上で書いたように
複利効果を活かして
時間をかけて運用するのが
よさそうです。

株式投資の場合ですと
リターンを年5％程度で想定する事が多いですが、
私のような一般人は
この程度の利回りを目指していくのが
現実的な方法ではないでしょうか？

利益を年5％
運用開始時点での資金を100万円
yを資産総額、xを投資期間の長さ[年]とすれば
資産総額yは

$$ y=1000000 \times 1.05^x $$

このように書けます。

年5％といえどもそれが続けば
資産は指数関数的に増えるわけですから
侮ることはできません。

実際の株式相場は
年によっては大きく上がったり
下がったりするので
現実にはコンスタントに年5％とは
いかないでしょうが、
世界の経済がこれからも成長するなら
長期的には利益が出る可能性が
期待できます。
（あくまで利益が『期待できる』のであって利益を保証するわけではありません・・・）

2020年最初の記事
読んで頂きありがとうございました！
では、今日はこの辺で失礼致します。